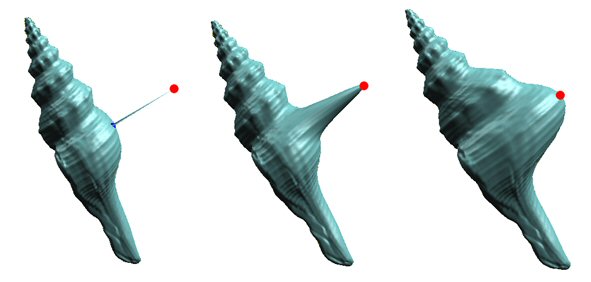
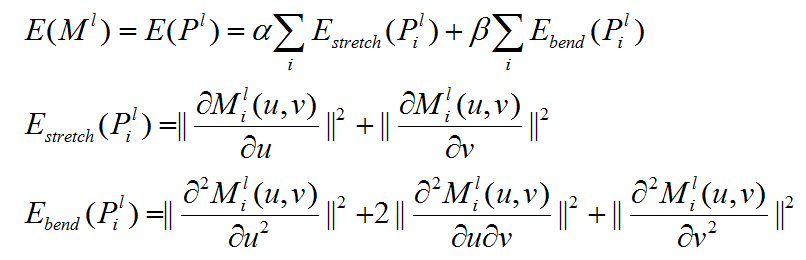A central concern when modeling surfaces that change dynamically is to identify how different points on a surface relate to each other during changes and how the movement of any given point (or part of the surface) affects the movements of others.
Impact of changing a point on a surface on its neighboring points.
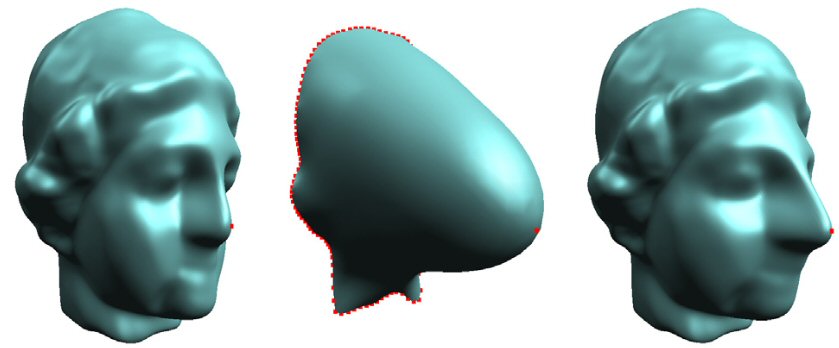
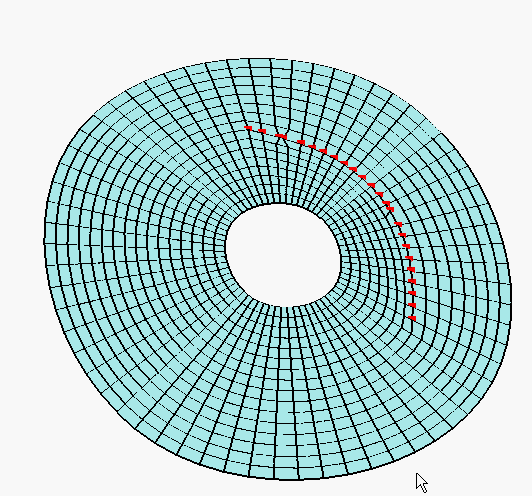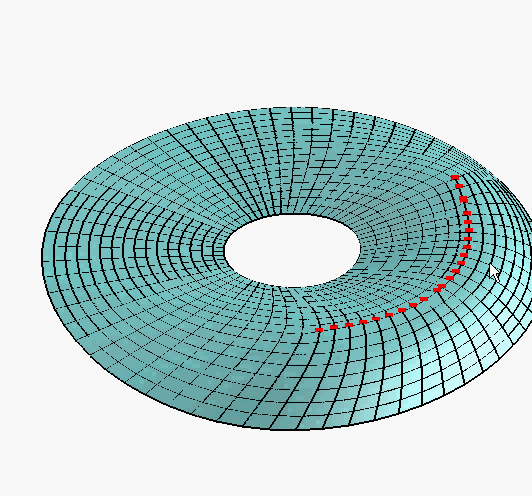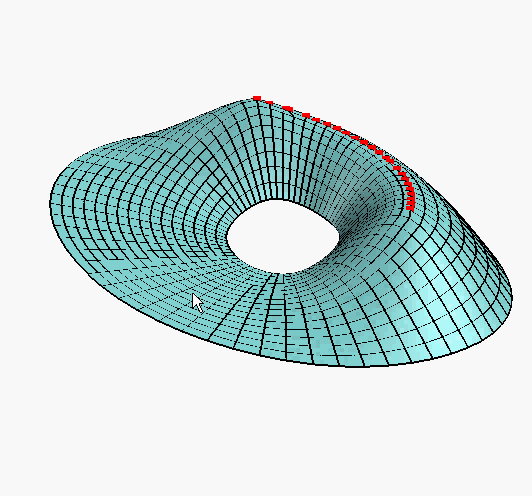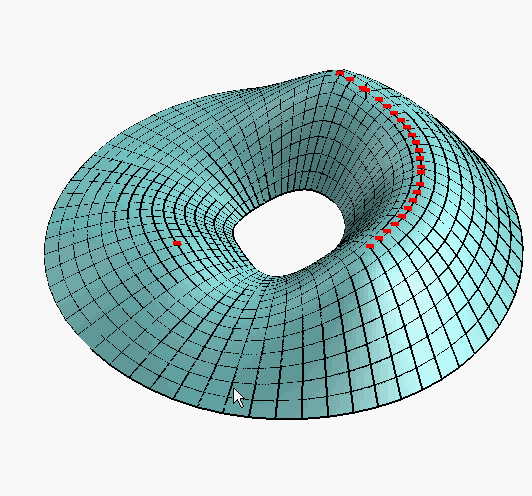
The trick is to find an optimal solution without smoothing out the details. In the example below if naive optimization is applied to Venus’ head using the constraints marked by the red points, the result will appear as shown in the middle image: an amorphous blob with no resemblance to the original. A more careful approach allows us to edit the nose without losing the face details as shown in the rightmost image.
Optimization can wipe out details of the object when naively applied.
Variational modeling entails finding optimal solutions to energy minimization problems in the presence of constraints. Commonly used energy functionals are combinations of stretching and bending energies:
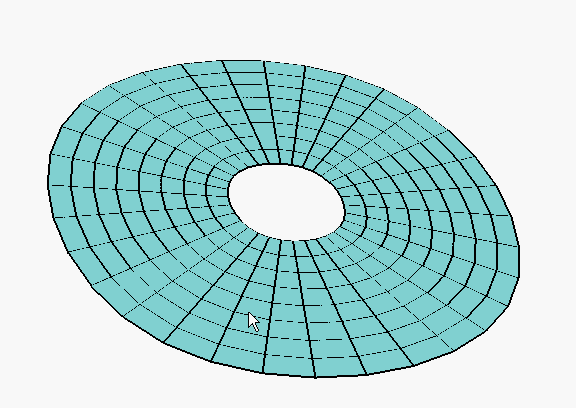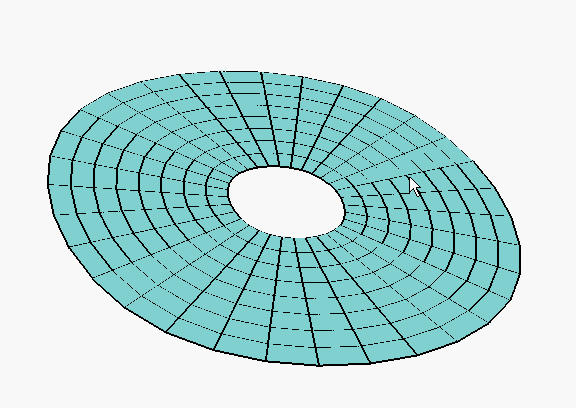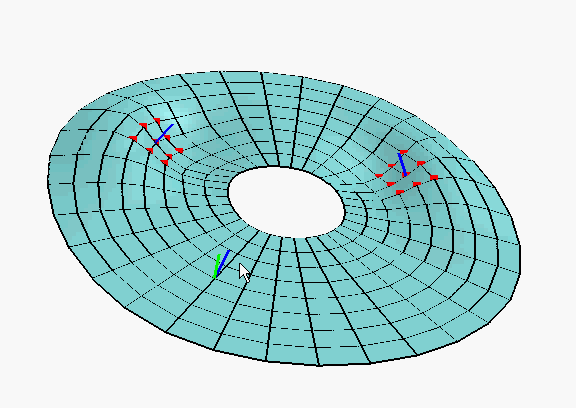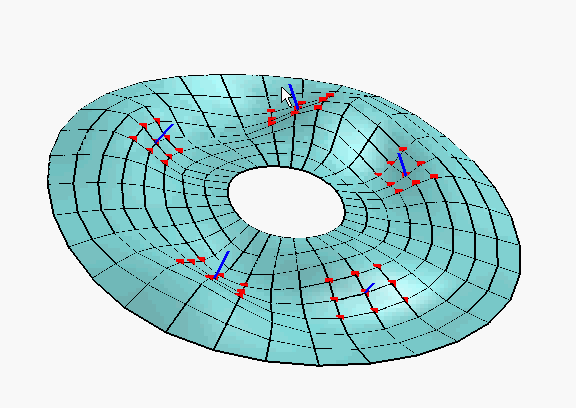
A surface represented as a multi-resolution mesh sequence can be interactively modified using point, curve, and normal constraints.
Interactive editing with point and curve constraints.
Interactive editing with normal constraints.
For further details see Detail-Preserving Variational Surface Design with Multiresolution Constraints.